Não existem derrotas que abalem aquele que nasceu para vencer.
Bjjoss Valeuuu!!!
Jussara Andrade
Teoria da Matemática -
Você que tem dificuldade na Matemática // não se preocupe, pois entrou no lugar certo. Este BLOG foi feito para tirar todas suas duvidadas dessa matéria um pouco complicada. Aqui você encontrara dicas, videos e muito mais.
quarta-feira, 30 de novembro de 2011
E pra vocês deixo::
E com vocês eu deixo meu melhor sorriso, meu maior abraço, minha melhor história, minha melhor intenção, toda minha compreensão. E da minha amizade, a maior porção.
A Geometria do AMOR!!
Todo mundo, um dia, já ouviu falar que as retas paralelas se cruzam no infinito. Eu inclusive, já acreditei nisso. Sempre usavam como exemplo as viagens que fazemos por rodovias retas. Lá na frente, parece mesmo que elas vão se cruzar, mesmo sabendo que viajando de São Paulo para Goiás, podemos dormir por horas no carro e estaremos perfeitamente seguros, como estávamos antes de cochilar.
Retas paralelas têm a mesma inclinação e podemos passar uma reta perpendicular as duas ao mesmo tempo. Não sei se essa é a definição exata de retas paralelas, mas isso já basta para que você me compreenda.
Quero falar de pessoas e de inclinações. Você, com certeza já ouviu máximas como “dois bicudos não se bicam” e sua mãe já deve ter te dado conselhos sobre procurar uma pessoa que é diferente de você usando aquele velho argumento de que um deve completar o outro e que se você e o seu parceiro fossem muito parecidos a vida seria monótona, sem emoção. Acontece que, teimosos como somos, insistimos em procurar aqueles que mais combinam com o nosso perfil, que goste das mesmas coisas, e acreditamos fortemente que um dia iremos encontrar. Ou seja, procuramos pessoas com a mesma inclinação e insistimos que mesmo que demore, um dia vamos “cruzar” com uma delas por aí. Se você pensa assim, sinto muito, mas tenho uma péssima notícia: A geometria proíbe.
Quê? O que a geometria tem a ver com a minha vida?
Calma, calma. Eu explico.
Imaginemos que em um determinado ponto no espaço, as retas se cruzam. Você finalmente encontrou quem procurava. Portanto, há um ângulo maior que zero, entre vocês. Certo? Peguemos agora, uma reta, aquela que é perpendicular a você e a outra pessoa. Agora, some os ângulos do interior do triângulo formado.
Opa… Como assim? Deu maior que 180 graus.
Pois é, isso é um Absurdo. Logo, não insista. Não vale a pena ficar esperando aquela pessoa que gosta dos mesmos filmes que você, que tem a mesma personalidade e que tem opiniões similares porque simplesmente as coisas não vão dar certo. Nem que demore muito, nem no infinito, você vai conseguir “cruzar” com essa pessoa, já que, como eu disse, a geometria proíbe.
Geometria e corpos redondos:
Os sólidos geométricos são separados em:
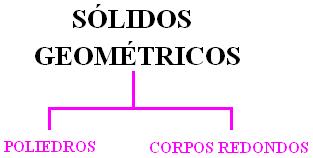
Os sólidos geométricos que representam os corpos redondos são:
• Cilindro
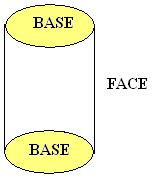
• Cone
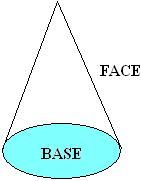
• Esfera
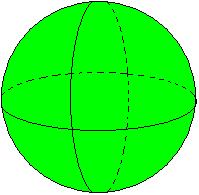
Essas figuras possuem características semelhantes, como:
São sólidos que possuem as bases em forma de círculo.
São sólidos que colocados em um plano inclinado rolam.
Podemos observar alguns objetos que possuem as formas de um corpo redondo, como:
Cilindro: cano, tubo de caneta, rolo de papel higiênico, canudo, copo, etc.
Cone: Casquinha de sorvete, chapéu de festa de criança, etc.
Esfera: bola de futebol, bolinha de gude, etc.
Os corpos redondos e os poliedros possuem características semelhantes. Ao compararmos o cilindro com o prisma percebemos que possuem duas bases e se compararmos o cone com a pirâmide percebemos que possuem apenas uma base e todas as arestas que saem dessa base se encontram em um único vértice.
Essas semelhanças serão notadas no cálculo do volume de casa sólido geométrico.

Os sólidos geométricos que representam os corpos redondos são:
• Cilindro
• Cone
• Esfera
Essas figuras possuem características semelhantes, como:
São sólidos que possuem as bases em forma de círculo.
São sólidos que colocados em um plano inclinado rolam.
Podemos observar alguns objetos que possuem as formas de um corpo redondo, como:
Cilindro: cano, tubo de caneta, rolo de papel higiênico, canudo, copo, etc.
Cone: Casquinha de sorvete, chapéu de festa de criança, etc.
Esfera: bola de futebol, bolinha de gude, etc.
Os corpos redondos e os poliedros possuem características semelhantes. Ao compararmos o cilindro com o prisma percebemos que possuem duas bases e se compararmos o cone com a pirâmide percebemos que possuem apenas uma base e todas as arestas que saem dessa base se encontram em um único vértice.
Essas semelhanças serão notadas no cálculo do volume de casa sólido geométrico.
domingo, 27 de novembro de 2011
Ângulo
O que é e como medir
Ângulo é a área entre duas semi-retas que se encontram.
Veja a figura abaixo:
OA e OB são semi-retas (infinitas, por definição). O é o ponto em que as duas semi-retas se encontram. A área contida entre estas duas semi-retas é o ângulo AÔB. A representação escrita funciona assim: o ponto em que as retas se encontram vai representada com um acento circunflexo ^.
Até que se obtivesse um ângulo totalmente aberto:
Continuando:
Se continuarmos até que o ponto A se junte ao ponto B, temos uma volta completa. Essa ângulo que deu a volta completa é a chamada de 360° (lê-se 360 graus).
A unidade de medida do ângulo, portanto, é o grau. Ele é dividido em minutos ('), que por sua vez são divididos em segundos ("):
1º = 60' (um grau é igual a 60 minutos)
1' = 60" (um minuto é igual a 60 segundos)
Fazer a transformação de medidas dos ângulos é tarefa simples e relativamente comum em geometria. Ela é necessária, por exemplo, para se fazerem operações com medidas de ângulos (graus, minutos e segundos).
Veja a figura abaixo:
 |
OA e OB são semi-retas (infinitas, por definição). O é o ponto em que as duas semi-retas se encontram. A área contida entre estas duas semi-retas é o ângulo AÔB. A representação escrita funciona assim: o ponto em que as retas se encontram vai representada com um acento circunflexo ^.
Medidas
Imagine que você pegue o ângulo acima e comece a aumentá-lo:  |
 |
Até que se obtivesse um ângulo totalmente aberto:
 |
Continuando:
 |
Se continuarmos até que o ponto A se junte ao ponto B, temos uma volta completa. Essa ângulo que deu a volta completa é a chamada de 360° (lê-se 360 graus).
A unidade de medida do ângulo, portanto, é o grau. Ele é dividido em minutos ('), que por sua vez são divididos em segundos ("):
1º = 60' (um grau é igual a 60 minutos)
1' = 60" (um minuto é igual a 60 segundos)
Fazer a transformação de medidas dos ângulos é tarefa simples e relativamente comum em geometria. Ela é necessária, por exemplo, para se fazerem operações com medidas de ângulos (graus, minutos e segundos).
Análise combinatória
Como calcular probabilidades
Para aprender como fazer cálculos de análise combinatória, útil para determinar probabilidades, veja um exercício resolvido:
Escrito há cerca de 3 mil anos, o "I - Ching" ou "Livro das Mutações" apresenta um conjunto de símbolos criados a partir de dois princípios (o masculino Yang, representado por uma linha inteira -, e o feminino Ying, representado por uma linha quebrada - - ).
Entre outras funções, esse conjunto de símbolos permitiria adivinhar o futuro, o que torna o livro muito popular ainda hoje em dia. A base do sistema é um conjunto de três símbolos montados com as linhas Ying e Yang, que se constróem do seguinte modo:
A essas figuras chamadas Pa-Kua (as Oito Mutações), atribuíam-se nomes, características, imagens, papéis numa estrutura familiar, além dos pontos cardeais, como se vê a seguir:
Combinando-se dois desses trigramas, obtém-se um hexagrama, figura de significado ainda mais amplo, que constitui a resposta do oráculo a uma pergunta de quem o consulta. Por exemplo:
Sem entrar nas questões de caráter filosófico ou oracular do I-Ching, podemos nos perguntar: quantos hexagramas é possível formar com cada dois trigramas?
Pensando de forma análoga, podemos considerar que se constrói um hexagrama escolhendo seis símbolos de um grupo de dois (linha inteira, linha quebrada). Assim, o total de símbolos será 26 = 64.
Usamos aqui um princípio multiplicativo que é a base da análise combinatória, um conjunto de procedimentos que sistematiza a contagem de agrupamentos.
Essa é a versão multiplicativa do princípio: para que ocorra o evento, todas as etapas devem ser cumpridas. Por exemplo: para se escolher um número de três algarismos, devemos escolher o algarismo das unidades e das dezenas e também das centenas - não se podem omitir quaisquer etapas. Se as etapas não forem sucessivas, mas alternativas, o princípio fica enunciado assim:
Um evento ocorre em n etapas, alternativas e independentes, de modo que a primeira etapa ocorre de k1 maneiras, a segunda etapa ocorre de k2 maneiras, ..., e a enésima etapa ocorre de k2. Então, o evento pode ocorrer de k12 + ... + Kn maneiras distintas.
Se, para o seu almoço, você pode escolher um lanche com ou sem maionese, então você pode escolher entre dois lanches!
Arranjos: são agrupamentos nos quais a ordem dos elementos é relevante. Três pessoas (A, B, C) que se inscrevem em um concurso que premia os dois primeiros lugares podem dar a esse concurso seis classificações distintas:
Observe que duas mesmas pessoas podem terminar o concurso de duas maneiras distintas.
O número de arranjos possíveis de p elementos tirados de um grupo de n elementos, com n p pode ser escrito como:
p pode ser escrito como:
Combinações: são agrupamentos em que a ordem dos elementos não é relevante. No exemplo anterior, se as pessoas A, B e C tivessem que se organizar para formar uma comissão de duas pessoas, só haveria três possibilidades : A e B, A e C, B e C. O número de combinações de p elementos tirados de um grupo de n elementos, com n p é:
p é:
As permutações são casos particulares de arranjos em que o número de elementos do agrupamento é igual ao número de elementos disponíveis:
A sistemática da análise combinatória não é novidade. Em toda a história do desenvolvimento matemático do homem aparecem registros de investigações nos cálculos de possíveis agrupamentos:
Na obra de Euclides (300 a.C.) há um método para se encontrar o valor de (1 + x)2;
Além da fórmula resolutiva para equações de 2o grau, Baskhara descreveu algumas situações práticas em que se permutam possibilidades - na poesia, na arquitetura e na medicina;
Trabalhos do início da Era Cristã relacionados à cabala analisam combinações e permutações entre números inteiros;
Astrônomos da Idade Média calculavam as possíveis conjunções entre dois, três, n planetas,
À época do Renascimento, a pressão das recentes descobertas e necessidades mercantis fizeram com que matemáticos europeus desenvolvessem a sistemática de combinatória na descrição de várias circunstâncias: as possibilidades de n pessoas se sentarem em torno de uma mesa, as combinações possíveis de fechaduras, os agrupamentos possíveis de objetos e, naturalmente, as chances nos jogos de azar.
Apesar de tantas outras motivações, foi o interesse pelos jogos de azar a grande motivação para o desenvolvimento da análise combinatória, nos trabalhos de Pascal e Fermat. Naturalmente, outros ramos da matemática usaram esse conhecimento e vieram a se desenvolver: a probabilidade, a teoria de grafos, os conjuntos e a criptologia. A chance de jogos como a MegaSena é um saber relacionado à análise combinatória.
Escrito há cerca de 3 mil anos, o "I - Ching" ou "Livro das Mutações" apresenta um conjunto de símbolos criados a partir de dois princípios (o masculino Yang, representado por uma linha inteira -, e o feminino Ying, representado por uma linha quebrada - - ).
Entre outras funções, esse conjunto de símbolos permitiria adivinhar o futuro, o que torna o livro muito popular ainda hoje em dia. A base do sistema é um conjunto de três símbolos montados com as linhas Ying e Yang, que se constróem do seguinte modo:
| 1o símbolo | 2o símbolo | 3o símbolo |
 |  |  |
A essas figuras chamadas Pa-Kua (as Oito Mutações), atribuíam-se nomes, características, imagens, papéis numa estrutura familiar, além dos pontos cardeais, como se vê a seguir:
| Norte | Nordeste | Leste | Sudeste |
| | | | |
| Sul | Sudoeste | Oeste | Noroeste |
| | | | |
Combinando-se dois desses trigramas, obtém-se um hexagrama, figura de significado ainda mais amplo, que constitui a resposta do oráculo a uma pergunta de quem o consulta. Por exemplo:
 |
Sem entrar nas questões de caráter filosófico ou oracular do I-Ching, podemos nos perguntar: quantos hexagramas é possível formar com cada dois trigramas?
| 1o trigrama | 2o trigrama | Total: 64 hexagramas |
| 8 possibilidades | 8 possibilidades |
Pensando de forma análoga, podemos considerar que se constrói um hexagrama escolhendo seis símbolos de um grupo de dois (linha inteira, linha quebrada). Assim, o total de símbolos será 26 = 64.
Usamos aqui um princípio multiplicativo que é a base da análise combinatória, um conjunto de procedimentos que sistematiza a contagem de agrupamentos.
O princípio fundamental da contagem
Um evento ocorre em n etapas, sucessivas e independentes, de modo que a primeira etapa ocorre de k1 maneiras, a segunda etapa ocorre de k2 maneiras, ..., e a enésima etapa ocorre de kn. Então, o evento pode ocorrer de k1, k2, ... .Kn maneiras distintas.Essa é a versão multiplicativa do princípio: para que ocorra o evento, todas as etapas devem ser cumpridas. Por exemplo: para se escolher um número de três algarismos, devemos escolher o algarismo das unidades e das dezenas e também das centenas - não se podem omitir quaisquer etapas. Se as etapas não forem sucessivas, mas alternativas, o princípio fica enunciado assim:
Um evento ocorre em n etapas, alternativas e independentes, de modo que a primeira etapa ocorre de k1 maneiras, a segunda etapa ocorre de k2 maneiras, ..., e a enésima etapa ocorre de k2. Então, o evento pode ocorrer de k12 + ... + Kn maneiras distintas.
Se, para o seu almoço, você pode escolher um lanche com ou sem maionese, então você pode escolher entre dois lanches!
Agrupamentos
De modo geral, pode-se resolver um grande número de situações de contagem usando os princípios fundamentais. No entanto, alguns conjuntos podem ser agrupados por critérios que facilitam a sua compreensão; compreender a que classe de agrupamento pertence a situação que estamos tratando pode facilitar muito a resolução.Arranjos: são agrupamentos nos quais a ordem dos elementos é relevante. Três pessoas (A, B, C) que se inscrevem em um concurso que premia os dois primeiros lugares podem dar a esse concurso seis classificações distintas:
| 1o lugar | 2o lugar |
| A | B |
| A | C |
| B | A |
| B | C |
| C | A |
| C | B |
Observe que duas mesmas pessoas podem terminar o concurso de duas maneiras distintas.
O número de arranjos possíveis de p elementos tirados de um grupo de n elementos, com n
 p pode ser escrito como:
p pode ser escrito como: |
Combinações: são agrupamentos em que a ordem dos elementos não é relevante. No exemplo anterior, se as pessoas A, B e C tivessem que se organizar para formar uma comissão de duas pessoas, só haveria três possibilidades : A e B, A e C, B e C. O número de combinações de p elementos tirados de um grupo de n elementos, com n
 p é:
p é: |
As permutações são casos particulares de arranjos em que o número de elementos do agrupamento é igual ao número de elementos disponíveis:
 |
A sistemática da análise combinatória não é novidade. Em toda a história do desenvolvimento matemático do homem aparecem registros de investigações nos cálculos de possíveis agrupamentos:
Apesar de tantas outras motivações, foi o interesse pelos jogos de azar a grande motivação para o desenvolvimento da análise combinatória, nos trabalhos de Pascal e Fermat. Naturalmente, outros ramos da matemática usaram esse conhecimento e vieram a se desenvolver: a probabilidade, a teoria de grafos, os conjuntos e a criptologia. A chance de jogos como a MegaSena é um saber relacionado à análise combinatória.
Assinar:
Comentários (Atom)
