Não existem derrotas que abalem aquele que nasceu para vencer.
Bjjoss Valeuuu!!!
Jussara Andrade
Você que tem dificuldade na Matemática // não se preocupe, pois entrou no lugar certo. Este BLOG foi feito para tirar todas suas duvidadas dessa matéria um pouco complicada. Aqui você encontrara dicas, videos e muito mais.
quarta-feira, 30 de novembro de 2011
E pra vocês deixo::
E com vocês eu deixo meu melhor sorriso, meu maior abraço, minha melhor história, minha melhor intenção, toda minha compreensão. E da minha amizade, a maior porção.
A Geometria do AMOR!!
Todo mundo, um dia, já ouviu falar que as retas paralelas se cruzam no infinito. Eu inclusive, já acreditei nisso. Sempre usavam como exemplo as viagens que fazemos por rodovias retas. Lá na frente, parece mesmo que elas vão se cruzar, mesmo sabendo que viajando de São Paulo para Goiás, podemos dormir por horas no carro e estaremos perfeitamente seguros, como estávamos antes de cochilar.
Retas paralelas têm a mesma inclinação e podemos passar uma reta perpendicular as duas ao mesmo tempo. Não sei se essa é a definição exata de retas paralelas, mas isso já basta para que você me compreenda.
Quero falar de pessoas e de inclinações. Você, com certeza já ouviu máximas como “dois bicudos não se bicam” e sua mãe já deve ter te dado conselhos sobre procurar uma pessoa que é diferente de você usando aquele velho argumento de que um deve completar o outro e que se você e o seu parceiro fossem muito parecidos a vida seria monótona, sem emoção. Acontece que, teimosos como somos, insistimos em procurar aqueles que mais combinam com o nosso perfil, que goste das mesmas coisas, e acreditamos fortemente que um dia iremos encontrar. Ou seja, procuramos pessoas com a mesma inclinação e insistimos que mesmo que demore, um dia vamos “cruzar” com uma delas por aí. Se você pensa assim, sinto muito, mas tenho uma péssima notícia: A geometria proíbe.
Quê? O que a geometria tem a ver com a minha vida?
Calma, calma. Eu explico.
Imaginemos que em um determinado ponto no espaço, as retas se cruzam. Você finalmente encontrou quem procurava. Portanto, há um ângulo maior que zero, entre vocês. Certo? Peguemos agora, uma reta, aquela que é perpendicular a você e a outra pessoa. Agora, some os ângulos do interior do triângulo formado.
Opa… Como assim? Deu maior que 180 graus.
Pois é, isso é um Absurdo. Logo, não insista. Não vale a pena ficar esperando aquela pessoa que gosta dos mesmos filmes que você, que tem a mesma personalidade e que tem opiniões similares porque simplesmente as coisas não vão dar certo. Nem que demore muito, nem no infinito, você vai conseguir “cruzar” com essa pessoa, já que, como eu disse, a geometria proíbe.
Geometria e corpos redondos:
Os sólidos geométricos são separados em:
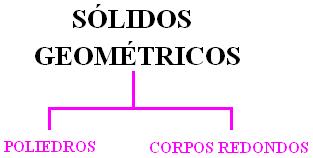
Os sólidos geométricos que representam os corpos redondos são:
• Cilindro
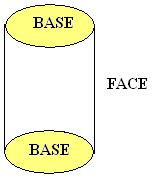
• Cone
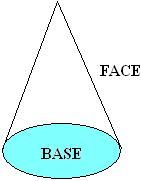
• Esfera
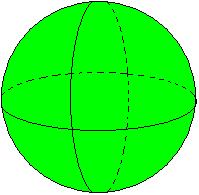
Essas figuras possuem características semelhantes, como:
São sólidos que possuem as bases em forma de círculo.
São sólidos que colocados em um plano inclinado rolam.
Podemos observar alguns objetos que possuem as formas de um corpo redondo, como:
Cilindro: cano, tubo de caneta, rolo de papel higiênico, canudo, copo, etc.
Cone: Casquinha de sorvete, chapéu de festa de criança, etc.
Esfera: bola de futebol, bolinha de gude, etc.
Os corpos redondos e os poliedros possuem características semelhantes. Ao compararmos o cilindro com o prisma percebemos que possuem duas bases e se compararmos o cone com a pirâmide percebemos que possuem apenas uma base e todas as arestas que saem dessa base se encontram em um único vértice.
Essas semelhanças serão notadas no cálculo do volume de casa sólido geométrico.

Os sólidos geométricos que representam os corpos redondos são:
• Cilindro
• Cone
• Esfera
Essas figuras possuem características semelhantes, como:
São sólidos que possuem as bases em forma de círculo.
São sólidos que colocados em um plano inclinado rolam.
Podemos observar alguns objetos que possuem as formas de um corpo redondo, como:
Cilindro: cano, tubo de caneta, rolo de papel higiênico, canudo, copo, etc.
Cone: Casquinha de sorvete, chapéu de festa de criança, etc.
Esfera: bola de futebol, bolinha de gude, etc.
Os corpos redondos e os poliedros possuem características semelhantes. Ao compararmos o cilindro com o prisma percebemos que possuem duas bases e se compararmos o cone com a pirâmide percebemos que possuem apenas uma base e todas as arestas que saem dessa base se encontram em um único vértice.
Essas semelhanças serão notadas no cálculo do volume de casa sólido geométrico.
domingo, 27 de novembro de 2011
Ângulo
O que é e como medir
Ângulo é a área entre duas semi-retas que se encontram.
Veja a figura abaixo:
OA e OB são semi-retas (infinitas, por definição). O é o ponto em que as duas semi-retas se encontram. A área contida entre estas duas semi-retas é o ângulo AÔB. A representação escrita funciona assim: o ponto em que as retas se encontram vai representada com um acento circunflexo ^.
Até que se obtivesse um ângulo totalmente aberto:
Continuando:
Se continuarmos até que o ponto A se junte ao ponto B, temos uma volta completa. Essa ângulo que deu a volta completa é a chamada de 360° (lê-se 360 graus).
A unidade de medida do ângulo, portanto, é o grau. Ele é dividido em minutos ('), que por sua vez são divididos em segundos ("):
1º = 60' (um grau é igual a 60 minutos)
1' = 60" (um minuto é igual a 60 segundos)
Fazer a transformação de medidas dos ângulos é tarefa simples e relativamente comum em geometria. Ela é necessária, por exemplo, para se fazerem operações com medidas de ângulos (graus, minutos e segundos).
Veja a figura abaixo:
 |
OA e OB são semi-retas (infinitas, por definição). O é o ponto em que as duas semi-retas se encontram. A área contida entre estas duas semi-retas é o ângulo AÔB. A representação escrita funciona assim: o ponto em que as retas se encontram vai representada com um acento circunflexo ^.
Medidas
Imagine que você pegue o ângulo acima e comece a aumentá-lo:  |
 |
Até que se obtivesse um ângulo totalmente aberto:
 |
Continuando:
 |
Se continuarmos até que o ponto A se junte ao ponto B, temos uma volta completa. Essa ângulo que deu a volta completa é a chamada de 360° (lê-se 360 graus).
A unidade de medida do ângulo, portanto, é o grau. Ele é dividido em minutos ('), que por sua vez são divididos em segundos ("):
1º = 60' (um grau é igual a 60 minutos)
1' = 60" (um minuto é igual a 60 segundos)
Fazer a transformação de medidas dos ângulos é tarefa simples e relativamente comum em geometria. Ela é necessária, por exemplo, para se fazerem operações com medidas de ângulos (graus, minutos e segundos).
Análise combinatória
Como calcular probabilidades
Para aprender como fazer cálculos de análise combinatória, útil para determinar probabilidades, veja um exercício resolvido:
Escrito há cerca de 3 mil anos, o "I - Ching" ou "Livro das Mutações" apresenta um conjunto de símbolos criados a partir de dois princípios (o masculino Yang, representado por uma linha inteira -, e o feminino Ying, representado por uma linha quebrada - - ).
Entre outras funções, esse conjunto de símbolos permitiria adivinhar o futuro, o que torna o livro muito popular ainda hoje em dia. A base do sistema é um conjunto de três símbolos montados com as linhas Ying e Yang, que se constróem do seguinte modo:
A essas figuras chamadas Pa-Kua (as Oito Mutações), atribuíam-se nomes, características, imagens, papéis numa estrutura familiar, além dos pontos cardeais, como se vê a seguir:
Combinando-se dois desses trigramas, obtém-se um hexagrama, figura de significado ainda mais amplo, que constitui a resposta do oráculo a uma pergunta de quem o consulta. Por exemplo:
Sem entrar nas questões de caráter filosófico ou oracular do I-Ching, podemos nos perguntar: quantos hexagramas é possível formar com cada dois trigramas?
Pensando de forma análoga, podemos considerar que se constrói um hexagrama escolhendo seis símbolos de um grupo de dois (linha inteira, linha quebrada). Assim, o total de símbolos será 26 = 64.
Usamos aqui um princípio multiplicativo que é a base da análise combinatória, um conjunto de procedimentos que sistematiza a contagem de agrupamentos.
Essa é a versão multiplicativa do princípio: para que ocorra o evento, todas as etapas devem ser cumpridas. Por exemplo: para se escolher um número de três algarismos, devemos escolher o algarismo das unidades e das dezenas e também das centenas - não se podem omitir quaisquer etapas. Se as etapas não forem sucessivas, mas alternativas, o princípio fica enunciado assim:
Um evento ocorre em n etapas, alternativas e independentes, de modo que a primeira etapa ocorre de k1 maneiras, a segunda etapa ocorre de k2 maneiras, ..., e a enésima etapa ocorre de k2. Então, o evento pode ocorrer de k12 + ... + Kn maneiras distintas.
Se, para o seu almoço, você pode escolher um lanche com ou sem maionese, então você pode escolher entre dois lanches!
Arranjos: são agrupamentos nos quais a ordem dos elementos é relevante. Três pessoas (A, B, C) que se inscrevem em um concurso que premia os dois primeiros lugares podem dar a esse concurso seis classificações distintas:
Observe que duas mesmas pessoas podem terminar o concurso de duas maneiras distintas.
O número de arranjos possíveis de p elementos tirados de um grupo de n elementos, com n p pode ser escrito como:
p pode ser escrito como:
Combinações: são agrupamentos em que a ordem dos elementos não é relevante. No exemplo anterior, se as pessoas A, B e C tivessem que se organizar para formar uma comissão de duas pessoas, só haveria três possibilidades : A e B, A e C, B e C. O número de combinações de p elementos tirados de um grupo de n elementos, com n p é:
p é:
As permutações são casos particulares de arranjos em que o número de elementos do agrupamento é igual ao número de elementos disponíveis:
A sistemática da análise combinatória não é novidade. Em toda a história do desenvolvimento matemático do homem aparecem registros de investigações nos cálculos de possíveis agrupamentos:
Na obra de Euclides (300 a.C.) há um método para se encontrar o valor de (1 + x)2;
Além da fórmula resolutiva para equações de 2o grau, Baskhara descreveu algumas situações práticas em que se permutam possibilidades - na poesia, na arquitetura e na medicina;
Trabalhos do início da Era Cristã relacionados à cabala analisam combinações e permutações entre números inteiros;
Astrônomos da Idade Média calculavam as possíveis conjunções entre dois, três, n planetas,
À época do Renascimento, a pressão das recentes descobertas e necessidades mercantis fizeram com que matemáticos europeus desenvolvessem a sistemática de combinatória na descrição de várias circunstâncias: as possibilidades de n pessoas se sentarem em torno de uma mesa, as combinações possíveis de fechaduras, os agrupamentos possíveis de objetos e, naturalmente, as chances nos jogos de azar.
Apesar de tantas outras motivações, foi o interesse pelos jogos de azar a grande motivação para o desenvolvimento da análise combinatória, nos trabalhos de Pascal e Fermat. Naturalmente, outros ramos da matemática usaram esse conhecimento e vieram a se desenvolver: a probabilidade, a teoria de grafos, os conjuntos e a criptologia. A chance de jogos como a MegaSena é um saber relacionado à análise combinatória.
Escrito há cerca de 3 mil anos, o "I - Ching" ou "Livro das Mutações" apresenta um conjunto de símbolos criados a partir de dois princípios (o masculino Yang, representado por uma linha inteira -, e o feminino Ying, representado por uma linha quebrada - - ).
Entre outras funções, esse conjunto de símbolos permitiria adivinhar o futuro, o que torna o livro muito popular ainda hoje em dia. A base do sistema é um conjunto de três símbolos montados com as linhas Ying e Yang, que se constróem do seguinte modo:
| 1o símbolo | 2o símbolo | 3o símbolo |
 |  |  |
A essas figuras chamadas Pa-Kua (as Oito Mutações), atribuíam-se nomes, características, imagens, papéis numa estrutura familiar, além dos pontos cardeais, como se vê a seguir:
| Norte | Nordeste | Leste | Sudeste |
| | | | |
| Sul | Sudoeste | Oeste | Noroeste |
| | | | |
Combinando-se dois desses trigramas, obtém-se um hexagrama, figura de significado ainda mais amplo, que constitui a resposta do oráculo a uma pergunta de quem o consulta. Por exemplo:
 |
Sem entrar nas questões de caráter filosófico ou oracular do I-Ching, podemos nos perguntar: quantos hexagramas é possível formar com cada dois trigramas?
| 1o trigrama | 2o trigrama | Total: 64 hexagramas |
| 8 possibilidades | 8 possibilidades |
Pensando de forma análoga, podemos considerar que se constrói um hexagrama escolhendo seis símbolos de um grupo de dois (linha inteira, linha quebrada). Assim, o total de símbolos será 26 = 64.
Usamos aqui um princípio multiplicativo que é a base da análise combinatória, um conjunto de procedimentos que sistematiza a contagem de agrupamentos.
O princípio fundamental da contagem
Um evento ocorre em n etapas, sucessivas e independentes, de modo que a primeira etapa ocorre de k1 maneiras, a segunda etapa ocorre de k2 maneiras, ..., e a enésima etapa ocorre de kn. Então, o evento pode ocorrer de k1, k2, ... .Kn maneiras distintas.Essa é a versão multiplicativa do princípio: para que ocorra o evento, todas as etapas devem ser cumpridas. Por exemplo: para se escolher um número de três algarismos, devemos escolher o algarismo das unidades e das dezenas e também das centenas - não se podem omitir quaisquer etapas. Se as etapas não forem sucessivas, mas alternativas, o princípio fica enunciado assim:
Um evento ocorre em n etapas, alternativas e independentes, de modo que a primeira etapa ocorre de k1 maneiras, a segunda etapa ocorre de k2 maneiras, ..., e a enésima etapa ocorre de k2. Então, o evento pode ocorrer de k12 + ... + Kn maneiras distintas.
Se, para o seu almoço, você pode escolher um lanche com ou sem maionese, então você pode escolher entre dois lanches!
Agrupamentos
De modo geral, pode-se resolver um grande número de situações de contagem usando os princípios fundamentais. No entanto, alguns conjuntos podem ser agrupados por critérios que facilitam a sua compreensão; compreender a que classe de agrupamento pertence a situação que estamos tratando pode facilitar muito a resolução.Arranjos: são agrupamentos nos quais a ordem dos elementos é relevante. Três pessoas (A, B, C) que se inscrevem em um concurso que premia os dois primeiros lugares podem dar a esse concurso seis classificações distintas:
| 1o lugar | 2o lugar |
| A | B |
| A | C |
| B | A |
| B | C |
| C | A |
| C | B |
Observe que duas mesmas pessoas podem terminar o concurso de duas maneiras distintas.
O número de arranjos possíveis de p elementos tirados de um grupo de n elementos, com n
 p pode ser escrito como:
p pode ser escrito como: |
Combinações: são agrupamentos em que a ordem dos elementos não é relevante. No exemplo anterior, se as pessoas A, B e C tivessem que se organizar para formar uma comissão de duas pessoas, só haveria três possibilidades : A e B, A e C, B e C. O número de combinações de p elementos tirados de um grupo de n elementos, com n
 p é:
p é: |
As permutações são casos particulares de arranjos em que o número de elementos do agrupamento é igual ao número de elementos disponíveis:
 |
A sistemática da análise combinatória não é novidade. Em toda a história do desenvolvimento matemático do homem aparecem registros de investigações nos cálculos de possíveis agrupamentos:
Apesar de tantas outras motivações, foi o interesse pelos jogos de azar a grande motivação para o desenvolvimento da análise combinatória, nos trabalhos de Pascal e Fermat. Naturalmente, outros ramos da matemática usaram esse conhecimento e vieram a se desenvolver: a probabilidade, a teoria de grafos, os conjuntos e a criptologia. A chance de jogos como a MegaSena é um saber relacionado à análise combinatória.
Álgebra
X? Y? Entenda os cálculos com letras
Para representar os problemas da vida real em linguagem matemática, muitas vezes utilizamos letras que substituem incógnitas (os valores que você não conhece, e quer descobrir). É aí que entram os famosos x, y, etc. O ramo da matemática que utiliza símbolos (normalmente letras do nosso alfabeto latino e do grego) para a resolução de problemas é chamado álgebra.
As equações são a aplicação mais conhecida dessa área da matemática.
Por exemplo, a área de um retângulo de base b e altura c é dada pela fórmula:
A = b . c
Esse conjunto de letras nada mais é que a representação de "fatos da vida real" por meio de números: a representa a área, b e c representam os lados do retângulo.
Essa fórmula vale para qualquer retângulo cuja área se deseja calcular.
Imagine que x represente um objeto, por exemplo, uma maçã. Então você faria:
"3 maçãs mais 7 maçãs"
Logicamente o resultado é "10 maçãs". Então:
O procedimento, como você viu, é simples: para somar números que acompanham incógnitas, basta somá-los, normalmente (desde que as incógnitas sejam iguais).
Agora suponha que x valha 17 maçãs. O resultado de nossa operação seria 170.
Para começar, é necessário saber o que é perímetro - é a soma de todos os lados de uma figura geométrica.
Como um lado foi chamado de x, o outro - que é o dobro - será 2x.
Nesse caso, o perímetro pode ser escrito como a soma dos 4 lados:
Logo:
Como o perímetro deve ser igual a 60, o único número que multiplicado por 6 resulta 60 é o número 10, logo:
Vimos, portanto, como utilizar letras para representar objetos e situações da vida real. no caso acima
a letra x representou o comprimento de um dos lados de um retângulo.
As equações são a aplicação mais conhecida dessa área da matemática.
Por exemplo, a área de um retângulo de base b e altura c é dada pela fórmula:
A = b . c
Esse conjunto de letras nada mais é que a representação de "fatos da vida real" por meio de números: a representa a área, b e c representam os lados do retângulo.
Essa fórmula vale para qualquer retângulo cuja área se deseja calcular.
Letras substituem valores iguais
Como você resolveria o seguinte cálculo?  |
Imagine que x represente um objeto, por exemplo, uma maçã. Então você faria:
"3 maçãs mais 7 maçãs"
Logicamente o resultado é "10 maçãs". Então:
 |
O procedimento, como você viu, é simples: para somar números que acompanham incógnitas, basta somá-los, normalmente (desde que as incógnitas sejam iguais).
Agora suponha que x valha 17 maçãs. O resultado de nossa operação seria 170.
Problemas resolvidos pela álgebra
Vamos descobrir quanto medem os lados de um retângulo em que um lado é o dobro do outro e cujo perímetro é igual a 60.  |
Para começar, é necessário saber o que é perímetro - é a soma de todos os lados de uma figura geométrica.
Como um lado foi chamado de x, o outro - que é o dobro - será 2x.
Nesse caso, o perímetro pode ser escrito como a soma dos 4 lados:
 |
Logo:
 |
Como o perímetro deve ser igual a 60, o único número que multiplicado por 6 resulta 60 é o número 10, logo:
 |
Vimos, portanto, como utilizar letras para representar objetos e situações da vida real. no caso acima
a letra x representou o comprimento de um dos lados de um retângulo.
sexta-feira, 18 de novembro de 2011
Piada
Livro de matemática
Por que o livro de matemática se suicidou??
Resp: Porque estava cheio de problemas.
Piada
Uma viagem de balão
Um homem viajando de balão se perdeu e resolveu parar em uma cidade para pedir informações:
-Por favor, onde estou?
- Você está nas coordenadas 30°s 45°w e o norte fica naquela direção .
- Você é físico?
- Como você sabe?
- É que você me deu uma resposta que mostra seu conhecimento do espaço ao seu redor.
Seguindo viagem o homem novamente se perde e pára em outra cidade.
- Por favor, onde estou?
- Você está em Cascavel, a igreja fica ali na frente, o prefeitura é virando aquela rua e se você seguir por esta estrada vai parar em Fortaleza.
- Você é engenheiro?
- Como você sabe?
- É que você me deu uma resposta que me mostra seu conhecimento da cidade.
Novamente perdido o baloneiro pára na terceira cidade.
-Por favor, onde estou?
-Você está em um balão.
-Você é matemático?
-Como você sabe?????
-É que você me deu uma resposta única, exata e que não me serve pra nada.
Equação
Nos tempos passados, as pessoas buscavam solucionar problemas do seu dia a dia, que envolviam matemática, através de processos aritméticos. Contudo, em certas situações esse processo não conseguia resolver os problemas que surgiam.
Com isso, passou-se a trabalhar com elementos algébricos, constituindo, assim, as equações que nada mais são do que expressões algébricas que representam uma determinada situação problema.
Entretanto, não basta conseguir esquematizar um problema apenas com expressões algébricas, é preciso saber resolver essas expressões algébricas. Para tanto, realizaram-se estudos acerca dos métodos de obtenção da solução das equações.
A obtenção da solução de uma equação é feita através de manipulações aritméticas, entretanto, envolvendo letras (incógnitas).
Mas qual o objetivo dessas letras em meio a números? As letras utilizadas nas expressões algébricas possuem a propriedade de representar qualquer número. Portanto, ao encontrarmos expressões que nos auxiliam a determinar a solução de um número para equações que possuem apenas letras, quer dizer que determinamos um método de obter a solução para qualquer tipo daquela equação.
Por exemplo, a solução de uma equação do tipo ax+b=0 é dada pela expressão x= -b/a. Veja que x é a incógnita, ou seja, o valor que queremos determinar e a, bsão os coeficientes dessa equação, representados por números quaisquer.
Importância do estudo da Matemática
A Matemática é uma ciência que relaciona o entendimento coerente e pensativo com situações práticas habituais. Ela compreende uma constante busca pela veracidade dos fatos através de técnicas precisas e exatas. Ao longo da história, a Matemática foi sendo construída e aperfeiçoada, organizada em teorias válidas e utilizadas atualmente.
Ela prossegue em sua constante evolução, investigando novas situações e estabelecendo relações com os acontecimentos cotidianos.
É considerada uma das ciências mais aplicadas em nosso cotidiano. Um simples olhar ao nosso redor e notamos a sua presença nas formas, nos contornos, nas medidas. As operações básicas são utilizadas constantemente, e os cálculos mais complexos são concluídos de forma prática e adequada de acordo com os princípios matemáticos postulados.
Possui uma estreita relação com as outras ciências, que buscam nos fundamentos matemáticos explicações práticas para suas teorias. Dizemos que a Matemática é a ciência das ciências.
Determinados assuntos ligados à Química, Física, Biologia, Administração, Contabilidade, Economia, Finanças, entre outras áreas de ensino e pesquisa, utilizam das bases matemáticas para estabelecerem resultados concretos e objetivos.
Atualmente a Matemática é subdividida, dessa forma constatou-se que ficaria mais fácil o seu aprendizado. Podemos organizá-la da seguinte forma:
Frase do Dia
O fato de viver não é suficiente para experimentar a realidade de ser
(Carlos Bernardo González Pecotche (Raumsol)

quarta-feira, 16 de novembro de 2011
Biografia Hipátia
Biografia
Hipátia era filha de Téon, um renomado filósofo, astrônomo, matemático, autor de diversas obras e professor em Alexandria.
Criada em um ambiente de idéias e filosofia, tinha uma forte ligação com o pai, que lhe transmitiu, além de conhecimentos, a forte paixão pela busca de respostas para o desconhecido. Diz-se que ela, sob tutela e orientação paternas, submetia-se a uma rigorosa disciplina física, para atingir o ideal helênico de ter a mente sã em um corpo são.
Hipátia estudou na Academia de Alexandria, onde devorava conhecimento: matemática, astronomia, filosofia, religião, poesia e artes. A oratória e a retórica também não foram descuidadas.
Alguns autores pensam que, quando adolescente, viajou para Atenas, para completar a educação na Academia Neoplatônica, onde não demorou a se destacar pelos esforços para unificar a matemática de Diofanto com o neoplatonismo de Amónio Sacas e Plotino, isto é, aplicando o raciocínio matemático ao conceito neoplatônico do Uno (mônada das mônadas). Ao retornar, já havia um emprego esperando por ela em Alexandria: seria professora na Academia onde fizera a maior parte dos estudos, ocupando a cadeira que fora de Plotino. Aos 30 anos já era diretora da Academia, sendo muitas as obras que escreveu nesse período.
Um dos seus alunos foi o notável filósofo e bispo Sinésio de Cirene (370 - 413), que lhe escrevia freqüentemente, pedindo-lhe conselhos. Através destas cartas, sabemos que Hipátia desenvolveu alguns instrumentos usados na Física e na Astronomia, entre os quais o hidrômetro.
Sabemos também que desenvolveu estudos sobre a Álgebra de Diofanto ("Sobre o Cânon Astronômico de Diofanto"), tendo escrito um tratado sobre o assunto, além de comentários sobre os matemáticos clássicos, incluindo Ptolomeu. Em parceria com o pai, escreveu um tratado sobre Euclides.
Ficou famosa por ser uma grande solucionadora de problemas. Matemáticos confusos, com algum problema em especial, escreviam-lhe pedindo uma solução. E ela raramente os desapontava. Obcecada pelo processo de demonstração lógica, quando lhe perguntavam porque jamais se casara, respondia que já era casada com a verdade.
combatendo as heresias, sobretudo o Nestorianismo, que negava a Divindade de Jesus Cristo e a Maternidade Divina de Maria.
Frase do Dia
Precisamos sempre mudar, renovarmo-nos, rejuvenescer; caso contrário, endurecemos.
(GOETHE)
Probleminhas
Problema 01: Uma vasilha cilíndrica circular com capacidade para 1 litro está cheia de suco.

De que forma pode ser feita a transferência de suco da vasilha maior para uma outra vasilha irregular com capacidade para 678 ml, de modo que ambas as vasilhas fiquem com exatamente 500 ml, sem usar outras vasilhas.
Corpos Redondos ; novo assunto
Os sólidos geométricos que representam os corpos redondos são:
• Cilindro

• Cone

• Esfera

Essas figuras possuem características semelhantes, como:
São sólidos que possuem as bases em forma de círculo.
São sólidos que colocados em um plano inclinado rolam.
Podemos observar alguns objetos que possuem as formas de um corpo redondo, como:
Cilindro: cano, tubo de caneta, rolo de papel higiênico, canudo, copo, etc.
Cone: Casquinha de sorvete, chapéu de festa de criança, etc.
Esfera: bola de futebol, bolinha de gude, etc.
Os corpos redondos e os poliedros possuem características semelhantes. Ao compararmos o cilindro com o prisma percebemos que possuem duas bases e se compararmos o cone com a pirâmide percebemos que possuem apenas uma base e todas as arestas que saem dessa base se encontram em um único vértice.
Essas semelhanças serão notadas no cálculo do volume de casa sólido geométrico.
• Cilindro
• Cone
• Esfera
Essas figuras possuem características semelhantes, como:
São sólidos que possuem as bases em forma de círculo.
São sólidos que colocados em um plano inclinado rolam.
Podemos observar alguns objetos que possuem as formas de um corpo redondo, como:
Cilindro: cano, tubo de caneta, rolo de papel higiênico, canudo, copo, etc.
Cone: Casquinha de sorvete, chapéu de festa de criança, etc.
Esfera: bola de futebol, bolinha de gude, etc.
Os corpos redondos e os poliedros possuem características semelhantes. Ao compararmos o cilindro com o prisma percebemos que possuem duas bases e se compararmos o cone com a pirâmide percebemos que possuem apenas uma base e todas as arestas que saem dessa base se encontram em um único vértice.
Essas semelhanças serão notadas no cálculo do volume de casa sólido geométrico.
quinta-feira, 10 de novembro de 2011
Frase do Dia -
Sábio é o ser humano que tem coragem de ir diante do espelho da sua alma para reconhecer seus erros e fracassos e utilizá-los para plantar as mais belas sementes no terreno de sua inteligência.
Augusto Cury
Álgebra Básica - Racionalização de frações
Como dito anteriormente (na lição retrasada), não se costuma deixar uma fração com raiz de qualquer ordem no denominador, ou seja, não pode ter raízes na parte de baixo de uma fração.
Para corrigirmos isso, usamos uma técnica chamada de "Racionalização de Frações".
Um tópico bem simples. Se você já tem conhecimento desta matéria pode passar adiante e fazer os exercícios de Potenciação de Radiciação.
Racionalização de Frações (Introdução)
Esta técnica consiste em multiplicar a fração dada por um número que não altere o seu valor (apenas a sua apresentação).
Pense comigo, qual o número que pode ser multiplicado por qualquer outro e não altera o valor deste outro número?
- Isso mesmo, 1 (um) :)
Qualquer número multiplicado por 1 continua com o mesmo valor, veja os exemplos:
Agora sim vamos ver Racionalização de Frações.
O primeiro caso é quando temos apenas uma raiz sozinha no denominador.
Vamos ver como se racionaliza uma fração aplicando em um exemplo. Temos a fração e queremos saber uma representação para este mesmo valor, mas sem nenhuma raiz em baixo.
e queremos saber uma representação para este mesmo valor, mas sem nenhuma raiz em baixo.
A técnica diz que devemos multiplicar esta fração por outra fração que tenha valor 1 para não alterar seu valor.
Esta fração deve ter seu denominador igual ao seu numerador e ambos igual ao denominador da fração a ser modificada, no caso .
.

 Pronto, achamos a fração procurada:
Pronto, achamos a fração procurada:
 Mais exemplos:
Mais exemplos:
O segundo acontece quando, além da raiz temos outro número somado à ela no denominador. Exemplo:
Para racionalizar este tipo de fração devemos, novamente, multiplicar por uma fração de valor 1. Formada pelo denominador da primeira apenas com o sinal do meio trocado.
Veja os exemplos:
O terceiro caso ocorre quando temos uma raiz dentro de outra raiz no denominador. Veja os exemplos:
Para resolver estes casos, vamos ter que calcular dois passos. Primeiro devemos multiplicar pela fração formada pela raiz do denominador com o sinal do meio trocado. Veja os exemplos abaixo:
Note que até agora só trabalhamos com raízes quadradas.
Veja no próximo tópico como fazer se for uma raiz diferente de quadrada.
Este último caso é o menos comum de todos, mas não quer dizer que não caia no vestibular também.
Ele ocorre quando temos uma raiz diferente de raiz quadrada no denominador. Veja uns exemplos:
 Sendo que o expoente do resultado
Sendo que o expoente do resultado  , deve ser 1.Vamos ver um exemplo:
, deve ser 1.Vamos ver um exemplo:
Agora faça os exercícios sobre potênciação e radiciação para testar se você obteve êxito neste estudo inicial.
Para corrigirmos isso, usamos uma técnica chamada de "Racionalização de Frações".
Um tópico bem simples. Se você já tem conhecimento desta matéria pode passar adiante e fazer os exercícios de Potenciação de Radiciação.
Racionalização de Frações (Introdução)
Esta técnica consiste em multiplicar a fração dada por um número que não altere o seu valor (apenas a sua apresentação).
Pense comigo, qual o número que pode ser multiplicado por qualquer outro e não altera o valor deste outro número?
- Isso mesmo, 1 (um) :)
Qualquer número multiplicado por 1 continua com o mesmo valor, veja os exemplos:
5 · 1 = 5
123 · 1 = 123
Também sabemos que qualquer fração que tenha o numerador (parte de cima da fração) igual ao denominador (parte de baixo da fração) vale 1:| Racionalização de Frações (1o caso) |
Vamos ver como se racionaliza uma fração aplicando em um exemplo. Temos a fração
A técnica diz que devemos multiplicar esta fração por outra fração que tenha valor 1 para não alterar seu valor.
Esta fração deve ter seu denominador igual ao seu numerador e ambos igual ao denominador da fração a ser modificada, no caso

Agora, efetuando esta multiplicação de frações (numerador de uma multiplica o numerador de outra, denominador de uma multiplica o denominador de outra):
| fração | racionalização |
| Racionalização de Frações (2o caso) |
Veja os exemplos:
Note que a fração grifada em azul nos cálculos acima que é a fração que você deve multiplicar.
Ela é igual à parte de baixo da fração que estamos racionalizando, mas com sinal do termo que tem raiz, trocado.
| Racionalização de Frações (3o caso) |
| Ué, mas ainda tem uma raiz no denominador. - Isso mesmo, agora a gente aplica o 1° caso nesse resultado. | |
Veja no próximo tópico como fazer se for uma raiz diferente de quadrada.
| Racionalização de Frações (4o caso) |
Ele ocorre quando temos uma raiz diferente de raiz quadrada no denominador. Veja uns exemplos:
Para resolver este tipo de questão, novamente devemos multiplicar esta fração por uma que valha 1 e nos seja conveniente (que retire a raiz do denominador).
Esta fração conveniente será achada através da seguinte propriedade:
| Este será o exemplo que iremos desenvolver. Primeiro iremos transformar a raiz do denominador em potência | |||
| Pronto, agora em cima deste O expoente que procuramos é | |||
|
Assinar:
Comentários (Atom)


